Ronald Mapamula ™ @rmapamula There are only three colors, ten digits, and seven notes, it’s what we do with them that’s #important. #Leadership #wisdom
The Babylonians
It all started around 3000 BC with the Babylonians. They were one of the world’s first civilisations, and came up with some great ideas like agriculture, irrigation and writing. They plotted the paths of the Sun, the Moon and the planets, and recorded them on clay tablets (which you can still see in the British Museum). To the Babylonians we owe the modern ideas of angle, including the way that the circle is divided up into 360 degrees (owing to a small miscalculation, one per day). We also owe the Babylonians for the rather less pleasant invention of the (dreaded) taxman. And this was one of the reasons that the Babylonians needed to solve quadratic equations.
if  is the length of the side of the field,
is the length of the side of the field, 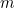 is the amount of crop you can grow on a square field of sidelength 1, and
is the amount of crop you can grow on a square field of sidelength 1, and  is the amount of crop that you can grow, then
is the amount of crop that you can grow, then
![\[ c = m x^2. \]](https://plus.maths.org/MI/393cd729e6bbe51ee24aedcdb865e310/images/img-0004.png) |
Quadratic equations and areas are linked together like brothers and sisters in the same family. However, at the moment we don’t have to solve anything – until the tax man arrives, that is! Cheerily he says to the farmer “I want you to give me  crops to pay for the taxes on your farm.” The farmer now has a dilemma: how big a field does he need to grow that amount of crop? We can answer this question easily, in fact
crops to pay for the taxes on your farm.” The farmer now has a dilemma: how big a field does he need to grow that amount of crop? We can answer this question easily, in fact
![\[ x = \sqrt { \frac{c}{m} }. \]](https://plus.maths.org/MI/393cd729e6bbe51ee24aedcdb865e310/images/img-0005.png) |
01 uses of a quadratic equation
5 Basic Needs (according to Glasser) o Fun o Freedom o Power o Belonging o Survival
Recognizing Factoring Patterns
Quadratic equations describe the motion of a baseball after it connects with a bat, and the acceleration of gravity at the Earth’s orbit.
A composite expression is similar in that it can be written as the product of two or more expressions. For example: x2 + 3x + 2 is composite because it can be written as (x + 1)(x + 2). (Recall that the FOIL Method shows that (x + 1)(x + 2) is equivalent to x2 + 3x + 2.) Here, (x + 1) and (x + 2) are factors of x2 + 3x + 2.
In general, a number is a factor of another number if the first number can divide the second without a remainder. Similarly, an expression is a factor of another expression if the first can divide the second without a remainder.
Definition
A prime number is a number greater than 1 which has only two positive factors: 1 and itself. For example, 11 is a prime number because its only positive factors are 1 and 11.
Factoring is a process by which a the factors of a composite number or a composite expression are determined, and the number or expression is written as a product of these factors. For example, the number 15 can be factored into: 1 * 15, 3 * 5, -1 * -15, or -3 * -5. The numbers -15, -5, -3, -1, 1, 3, 5, and 15 are all factors of 15 because they divide 15 without a remainder.
Factoring is an important process in algebra which is used to simplify expressions, simplify fractions, and solve equations. The next few lessons explain how to factor numbers, expressions, and equations.
Introduction To Factoring
A composite number is a number that can be written as the product of two positive integers other than 1 and the number itself. For example: 14 is a composite number because it can be written as 7 times 2. In this case, 7 and 2 are called factors of 14.

refresh on Solving Equations by Factoring
The Golden Arches ® Exposed!
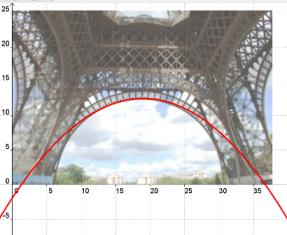
On the blog dy/dan, there was a recent discussion about the shape of a bridge. One commenter joked about the Golden Arches of McDonald’s as being the most famous parabolas in America. As I am teaching quadratic modeling in College Algebra right now, I though I would find an equation for these parabolas. The problem is that the Golden Arches are not parabolas.




Angle- The amount of turn between two straight lines that have a common end point (the vertex).